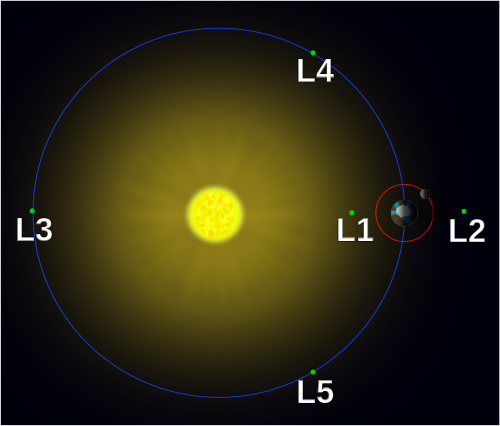
ラグランジュ点（ラグランジュポイント）とは？ 5つの平衡点をわかりやすく解説
シミュレーション動画で安定・不安定の違いを直感的に理解できます
ラグランジュ点（ラグランジュポイント）とは、太陽と地球のように重力で互いに周回する2天体の重力と遠心力が釣り合う5つの平衡点（L1〜L5）のことです。 宇宙望遠鏡JWSTの配置場所（L2）やトロヤ群小惑星の集まる場所（L4・L5）として知られています。
安定なラグランジュ点（L4）の周りに小天体をばらまくと何が起こるか？ まずは動画をご覧ください。
L4（安定）周辺の小天体 — 多くがとどまり続ける（質量比100）
安定な平衡点では小天体がとどまり、不安定な平衡点ではバラバラに散ります。 この違いを、以下で5つの点それぞれについて見ていきます。
5つのラグランジュ点の位置と特徴
L1〜L3は2天体を結ぶ直線上にあり、いずれも不安定（少しずれると離れていく）。 L4・L5は2天体と正三角形を形成する位置にあり、質量比が約25倍以上のとき安定（ずれても戻ってくる）になります。
| 点 | 位置 | 安定性 | 代表的な利用例 |
|---|---|---|---|
| L1 | 2天体の間 | 不安定 | SOHO（太陽観測） |
| L2 | 小天体の外側 | 不安定 | JWST（宇宙望遠鏡） |
| L3 | 大天体の外側 | 不安定 | （利用例なし） |
| L4 | 前方60度（正三角形） | 条件付き安定 | トロヤ群小惑星 |
| L5 | 後方60度（正三角形） | 条件付き安定 | トロヤ群小惑星 |
シミュレーションで見る安定性
各ラグランジュ点の周辺に多数の小天体を配置し、時間発展を見ることで安定性を可視化します。 太陽と地球の質量比は100倍に設定しています。
色の凡例
● 黄色 = 太陽（重い方の天体）
● 青 = 地球（軽い方の天体）
★ 黒 = ラグランジュ点
· 赤 = テスト用の小天体
L1 — 不安定 不安定
太陽と地球を結ぶ直線上にあるL1。周囲に配置した小天体はバラバラに散り、 太陽の周りを楕円軌道で回るものと、地球の周りをしばらく回るものに分かれます。
L1周辺の小天体の時間発展（質量比100）
L2 — 不安定 不安定
地球の外側にあるL2。ほとんどの小天体が遠心力によってふっ飛ばされ、 しばらくすると戻ってきます。残りは地球の周りを回った後、徐々に太陽側へ移動します。
L2周辺の小天体の時間発展（質量比100）
L3 — 不安定 不安定
太陽を挟んで地球の反対側にあるL3。最初は軌道全体に広がるような動きを見せ、 その後、小天体が地球に近づくとバラバラに散ります。 このようなわずかな初期値の違いが大きな結果の違いにつながる現象をカオスと呼びます。
L3周辺の小天体の時間発展 — カオス的挙動が見られる（質量比100）
L4 — 条件付き安定 条件付き安定
太陽と地球で正三角形を作る、地球の進行方向前方の頂点がL4です。 質量比100は安定条件（約25倍以上）を満たすため、多くの小天体がL4周辺にとどまります。 とどまっている小天体は「そら豆」のような軌道を描くことが知られています。
L4周辺の小天体の時間発展 — 多くがL4付近にとどまる（質量比100）
回転座標系で見ると、小天体がそら豆型の軌道を速度を変えながら周回していることがわかります。
L4周辺の運動（回転座標系）— そら豆軌道が確認できる
L5 — 条件付き安定 条件付き安定
L4と対称な位置にある、地球の進行方向後方の頂点がL5です。 L4と同じ条件付き安定の点であり、質量比100では安定な平衡点となります。
L5周辺の小天体の時間発展（質量比100）
質量比による安定・不安定の変化
Routhの安定条件（質量比 ≥ 約25）
L4とL5が安定な平衡点となる条件は、大きい方の天体の質量が小さい方の約25倍以上であることです。 正確には、質量比 m1/m2 > (25+3√69)/2 ≈ 24.96 というRouthの安定条件を満たす必要があります。 太陽-地球系（質量比 ≈ 333,000）や太陽-木星系（質量比 ≈ 1,047）はこの条件を大きく満たすため、 トロヤ群小惑星がL4・L5に安定して存在できます。
ギリギリ安定（質量比＝26） 安定
質量比100のときより安定性は弱まっていますが、それでもL4は安定な平衡点です。 小天体の軌道の広がりが大きくなっていることに注目してください。
L4周辺の時間発展（質量比26）— ギリギリ安定
不安定（質量比＝20） 不安定
質量比が安定条件を下回ると、L4は不安定な平衡点に変わります。 しばらく経つとほとんどの小天体がL4周辺の軌道から外れてしまいます。
L4周辺の時間発展（質量比20）— 不安定化
なぜL4・L5は安定なのか
コリオリ力の役割
L4・L5の安定性を理解するには、回転座標系で現れるコリオリ力が鍵となります。 回転座標系では、重力と遠心力に加えて、物体の速度に比例したコリオリ力が作用します。 L4・L5からずれた小天体は、コリオリ力によって平衡点の周囲を周回する方向に力を受け、 結果として平衡点から離れることなく、そら豆型の閉じた軌道を描きます。
有効ポテンシャルと「極大なのに安定」の理由
直感に反して、L4・L5は有効ポテンシャルの極大点（山頂）に位置します。 通常なら不安定ですが、コリオリ力はポテンシャルでは表現できない速度依存の力であり、 線形安定性解析を行うとRouthの安定条件下で全固有値が純虚数となり安定が示されます。
数学的な証明を読む →実際の利用例
| ラグランジュ点 | 探査機・天体 | なぜその点？ |
|---|---|---|
| 太陽-地球 L1 | SOHO, DSCOVR | 太陽と地球の間で常時太陽観測が可能 |
| 太陽-地球 L2 | JWST, Planck, Gaia | 太陽・地球・月を背にして深宇宙観測に最適 |
| 太陽-木星 L4/L5 | トロヤ群小惑星（1万個以上） | 安定な平衡点で数十億年とどまれる |
| 地球-月 L2 | 鵲橋（中国） | 月の裏側との通信中継 |
L1・L2は不安定ですが、ハロー軌道やリサジュー軌道に乗せ、わずかな燃料で軌道修正（ステーションキーピング）することで長期間とどまれます。 ラグランジュ点の概念はオイラー（1767年、L1〜L3）とラグランジュ（1772年、L4・L5）が発見し、1906年にトロヤ群小惑星「アキレス」の観測で初めて実証されました。
よくある質問
ラグランジュポイント（ラグランジュ点）とは何ですか？
ラグランジュポイント（ラグランジュ点）とは、太陽と地球のように重力で互いに周回する2天体の重力と遠心力が釣り合う5つの平衡点（L1〜L5）のことです。 この点に置かれた小さな物体は、2天体に対して相対的に静止できます。 JWSTやSOHOなどの宇宙望遠鏡の配置場所として実際に利用されています。
ラグランジュ点はどの天体系にもあるのか？
はい。太陽と地球、地球と月、太陽と木星など、重力で互いに周回する2天体の系であれば 必ず5つのラグランジュ点（L1〜L5）が存在します。 ただし、L4・L5の安定性は質量比によって異なり、質量比が約25倍未満の場合は不安定になります。
L4/L5が安定になる質量比の正確な値は？
Routhの安定条件により、大きい方の天体の質量が小さい方の約25倍以上 （正確には m1/m2 > (25+3√69)/2 ≈ 24.96）であるとき、 L4・L5は安定な平衡点になります。 太陽-地球系（約33万倍）や太陽-木星系（約1,047倍）はこの条件を十分に満たしています。
ラグランジュ点に物体を置いたら永遠にとどまるのか？
L4・L5が安定条件を満たす場合でも、物体はラグランジュ点に静止するのではなく、 そら豆型の軌道（リサジュー軌道やハロー軌道）を描いて周回します。 L1〜L3は不安定なので、JWSTなどの人工衛星は定期的な軌道修正（ステーションキーピング）を行っています。
なぜJWSTはL2に配置されたのか？
ジェイムズ・ウェッブ宇宙望遠鏡（JWST）は太陽-地球系のL2に配置されています。 L2は地球から見て太陽の反対側にあり、太陽シールドで太陽・地球・月からの光や熱を 同時に遮蔽できるため、赤外線観測に最適な極低温環境を維持できます。
ラグランジュ点とスペースコロニーの関係は？
ジェラルド・オニールが1970年代に提唱したスペースコロニー構想では、 地球-月系のL4またはL5が建設候補地とされています。 安定な平衡点であるため少ないエネルギーで位置を維持でき、 地球・月の両方にアクセスしやすい利点があります。 L5協会（現・全米宇宙協会）という推進団体も設立されました。
トロヤ群小惑星はなぜL4/L5に集まるのか？
トロヤ群小惑星は太陽-木星系のL4・L5付近に集まっています。 木星の質量は太陽の約1/1000で、安定条件（質量比 ≥ 約25）を大きく満たすため、 L4・L5が安定な平衡点となり、小惑星が数十億年にわたって留まることができます。 NASAの探査機「ルーシー」が初の直接探査を行っています。
最終更新日: 2026年2月24日